[Algorithm] 백준 11660, 15724, 1749 : DP 누적합

알고리즘

[Algorithm] 백준 11660, 15724, 1749 : DP 누적합

sxunea 2024. 10. 17. 00:06

이번주에는 dp + 누적합을 위주로 풀고 있는데, dp는 뭐 ... 점화식이 8할이라 따로 전략을 기록해 놓을 건 없다. 하지만 누적합은 문제 풀이 방법이 대부분 비슷하니 이 참에 정리해놓자.

누적합이란

누적합(구간 합)은 배열에서 특정 범위의 합을 빠르게 계산하기 위해 사용하는 기법이다. 배열의 각 위치까지의 값을 미리 더해두고, 필요한 구간의 합을 빠르게 계산하는 방식으로, 주로 1차원 혹은 2차원 배열에서 사용된다.

주로 특정한 구간을 주고 합 / 최대 합을 구하는 문제가 자주 나오는데, 반복문을 계속 돌려서 모든 경우의 수를 계산해 합을 구하는 것보다 누적합 알고리즘을 떠올리면 훨씬 빠르게 풀 수 있음을 기억하자.

1차원 배열의 누적합

1차원 배열의 경우, 누적합을 구하려면 arr[i]까지의 합을 미리 계산해 sum[i]에 저장해둔다.

그러면 구간 [i, j]의 합은 다음과 같이 간단히 계산할 수 있다.

sum[i] = arr[0] + arr[1] + ... + arr[i]
구간 [i, j]의 합: sum[j] - sum[i-1]

2차원 배열의 누적합

2차원 배열에서는 좌표 (i, j)까지의 값을 미리 더해두는 방식을 사용한다. 구간의 합을 구할 때에는 누적된 값들로부터 특정 부분을 빼거나 더하는 방식으로 빠르게 계산할 수 있다.

2차원 배열은 그림으로 보고 이해하는 것이 편해서, 그림과 계산 방법을 그려왔다. 아래 첨부로 설명을 대신하겠다.

위와 같이 누적합 배열을 만들어놓고, 거기서 문제가 원하는 답을 구하는 풀이 방식이 보편적이다. 저 누적합 공식이 반복해서 쓰이므로 그 도출 방법과 식을 잘 알아두고 넘어가도록 하자. 그러면 이제는 관련 대표 문제를 풀어보자.

2차원 배열 누적합 문제 풀이

구간 합 구하기 5

fun main() = with(System.`in`.bufferedReader()) {
    val (n, m) = readLine().split(" ").map { it.toInt() }
    val arr = Array(n) {
        readLine().split(' ').map { it.toInt() }
    }
    val sb = StringBuilder()
    val map = Array(n + 1) { IntArray(n + 1) }
    for (i in 1..n) {
        for (j in 1..n) {
            map[i][j] = arr[i - 1][j - 1] + map[i - 1][j] + map[i][j - 1] - map[i - 1][j - 1]
        }
    }
    repeat(m){
        val line = readLine().split(" ").map { it.toInt() }
        val answer = map[line[2]][line[3]] - map[line[0]-1][line[3]] - map[line[2]][line[1]-1] + map[line[0]-1][line[1]-1]
        sb.appendLine(answer)
    }
    println(sb)
}

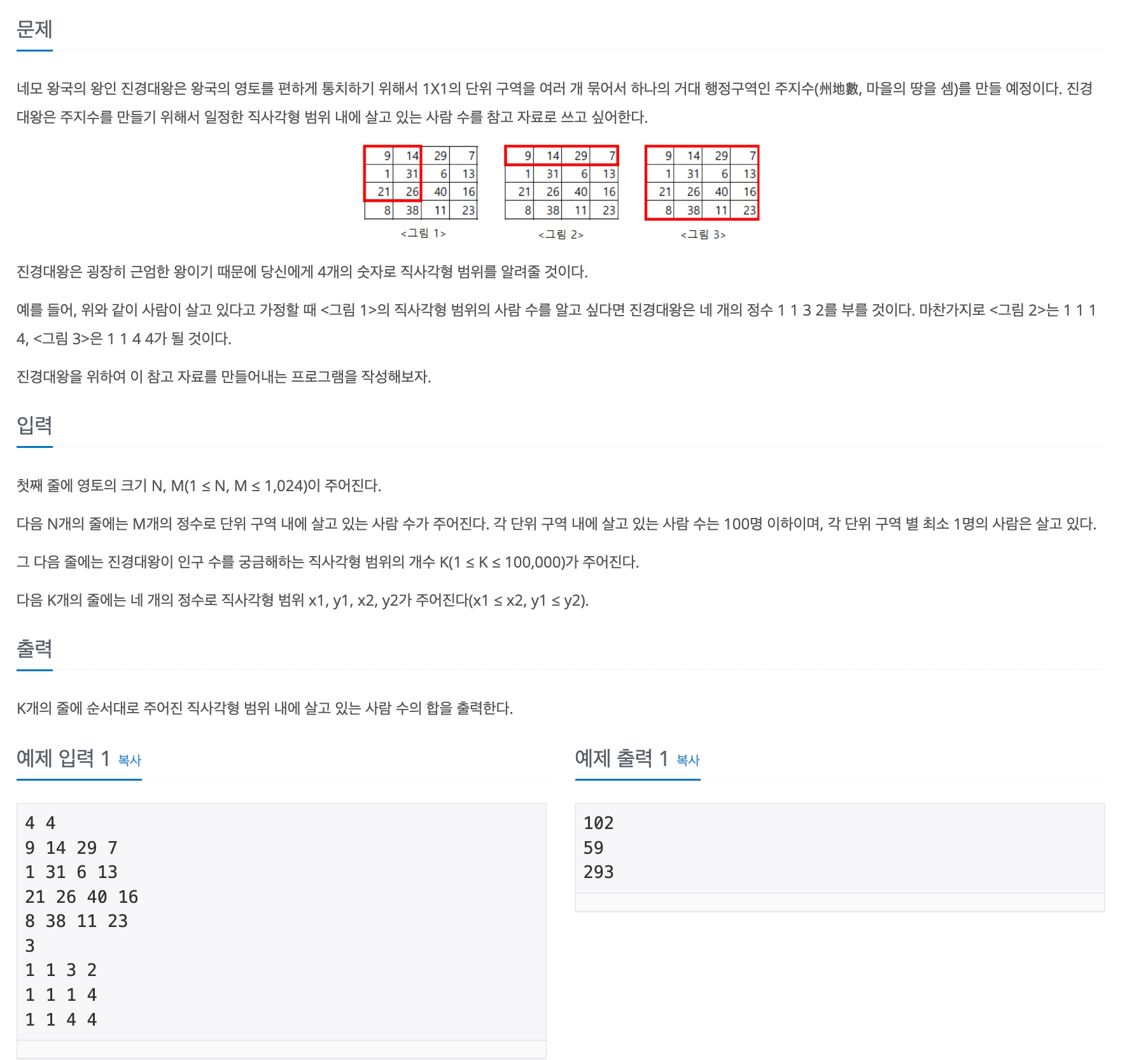
주지수

fun main() = with(System.`in`.bufferedReader()) {
    val (n, m) = readLine().split(" ").map { it.toInt() }

    val people = Array(n + 1) { IntArray(m + 1) }
    for (i in 1..n) {
        val row = readLine().split(" ").map { it.toInt() }
        for (j in 1..m) {
            people[i][j] = row[j - 1]
        }
    }

    val sum = Array(n + 1) { IntArray(m + 1) }
    for (i in 1..n) {
        for (j in 1..m) {
            sum[i][j] = people[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]
        }
    }

    val k = readLine().toInt()
    val output = StringBuilder()
    repeat(k) {
        val (x1, y1, x2, y2) = readLine().split(" ").map { it.toInt() }
        val result = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]
        output.appendLine(result)
    }

    print(output)
}

점수 따먹기

import kotlin.math.max

fun main() = with(System.`in`.bufferedReader()) {
    val (n, m) = readLine().split(" ").map { it.toInt() }
    val arr = Array(n) {
        readLine().split(' ').map { it.toInt() }
    }
    val map = Array(n + 1) { IntArray(m + 1) }
    for (i in 1..n) {
        for (j in 1..m) {
            map[i][j] = arr[i - 1][j - 1] + map[i - 1][j] + map[i][j - 1] - map[i - 1][j - 1]
        }
    }
    var answer = Int.MIN_VALUE
    for (i in 1..n) {
        for (j in 1..m) {
            for(ii in i..n){
                for(jj in j..m){
                    answer = max(answer, map[ii][jj] - map[ii][j-1] - map[i-1][jj] + map[i-1][j-1])
                }
            }
        }
    }
    println(answer)
}

세 문제가 실버~골드 로 레벨은 다르지만 결국 누적합 식을 세울 수만 있다면 빠르게 풀이할 수 있는 문제였다.